The a² has a coefficient of 3 and
since we can't factor this 3 out of the equation,
we want to multiply this coefficent with the constant c

Aa² - Ba - C

3a² - 23a - 36

3(36) = 108

next, we want to find the numbers that can be
multiplied to get 108 and added or subtracted to get 23

here, our numbers are 27 and 4
27(4) = 108   &   -27 + 4 = - 23

now, we'll rewrite the equation using our 27 and 4

3a² - 23a - 36

3a² + 4a - 27a - 36

break the equation in half and factor

3a2 + 4a a(3a + 4)

- 27a - 36 - 9(3a + 4)

our equation breaks down to

(a - 9)(3a + 4)

finally, we can finish this by solving for a₁ & a₂,
also called 'the roots'
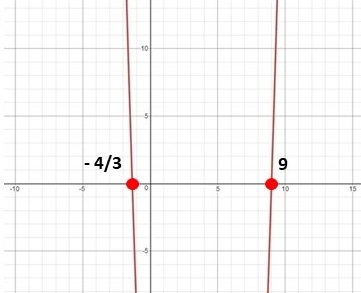
this is where the parabola crosses the x-axis

a - 9 = 0
a = 9

finding real roots

finding real roots

3a + 4 = 0 a = - 4 / 3

parabolas